2. CLASSIFYING SEQUENCES

Now that the harmonic sequence has been defined, how do we classify its various manifestations?
Let
us never allow it to slip from our minds that for all practical
purposes, the harmonic discourse is born of a single pair of harmonic
functions which permeates the entire system and which provides both the
engine and the goal: the dominant-tonic pair (V - I). It is essentially
from this perspective that we undertake the task of classification. All
harmonic sequences will therefore be perceived as the product
of imitation of the couple V - I which serves as an object of
reference without necessarily appearing within the sequence itself.
The imitation may refer to this pair:
- in the conventional sense (V - I):
Figure 17

regardless of the melodic motion (ascending fourth or descending fifth);
- in retrograde (I - V):
Figure 18

Note that a plagal perspective can be substituted for the tonal perspective (see, among others, examples 374 and 454). We know already that the tonal harmonic discourse includes many plagal gestures.
- or in a combination of both directions (I - V - I):
Figure 19

This
restriction excludes from our system of classification not only sequences
that present more than three chords in the model, but also those in which
the model (of two or three chords) does not correspond to the referential
pair. Another category thereby presents itself. These other sequences,
used much less frequently, draw on the same stereotypical fragments
of discourse (prefabricated harmonic material) which we have already
designated as formulas. In these cases, therefore, the model of the sequence
corresponds to one or another of those formulas, for example:

Example 384 : J.S. Bach : Little Preludes and Fugues, Fugue no 8 (mm 22-24)

Example 385 : D. Scarlatti : Sonata no 15, K. 175 (mm 61-63)


Example 386 : J.S. Bach : The Well-Tempered Clavier, vol. I, Prelude no 10, BWV 855 (mm 9-15)

Example 387 : W.A. Mozart : Fantasy, K. 475 (mm 128-131)

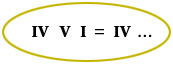
Example 388 : L.V. Beethoven : String quartet, op. 18, no 6, IV, La Malinconia (mm 21-29)

Example 389 : J.S. Bach : Sonata for flute and keyboard, BWV 1032, III, Allegro (mm 124-136)

Example 390 : W.A. Mozart : Symphony no 40, K. 550, IV (mm 157-177)
Type 1 sequence preceding the formula IV - V - I = IV

The model can even include several formulas combined:
Example 391 : W.A. Mozart : Viennese Sonatina no 2, I (mm 12-19)

Note
here that the reproduction, instead of repeating the three formulas in
the model, combines the last two into a single group (which corresponds
to a type 1 sequence, as we will see later).
Excluding
these cases, the proposed system of classification regroups, if not all, at least
most of the other sequences that appear in the discourse from Bach to
Wagner. Three criteria of classification permit the identification of 12 distinct types:
1. The (real) bass motion in the model.
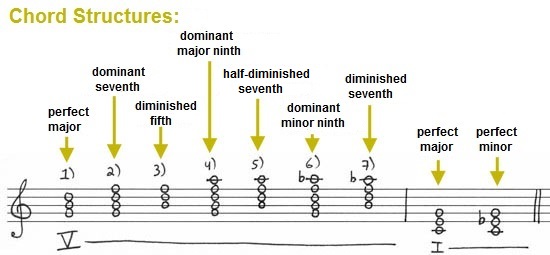
Here
we must remember that at least seven distinct chord structures (as
shown below) can fill the role of the dominant within the pair V - I:
Figure 20
2. The nature of the interval of progression of the harmonic model (a second or a third)
3. The direction of the interval of progression of the harmonic model (ascending or descending sequence)
Thus the twelve types of sequences are distributed according to the following table:
Figure 21

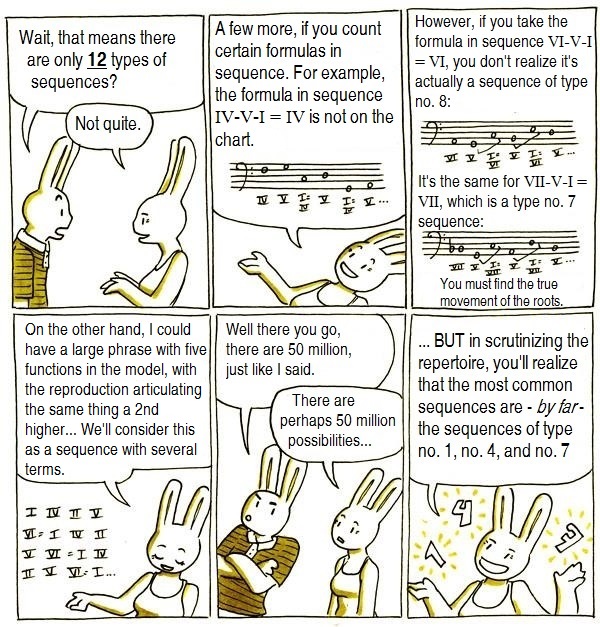
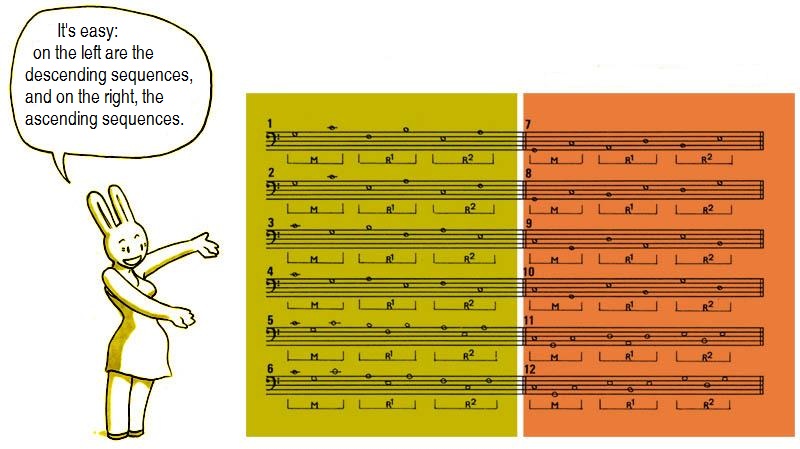
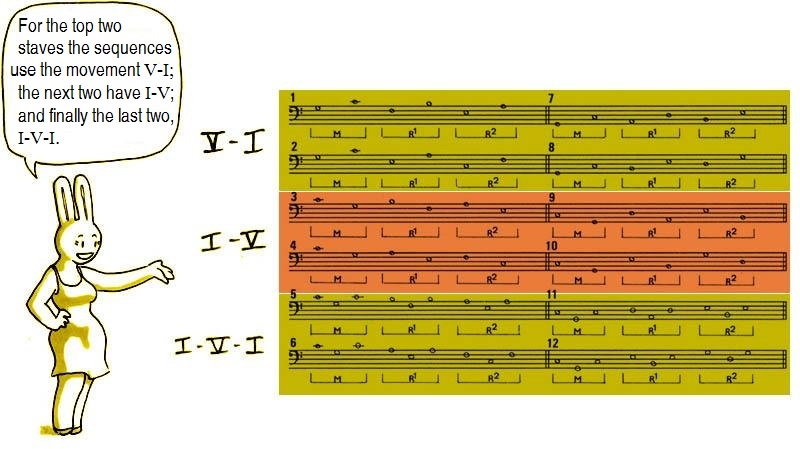
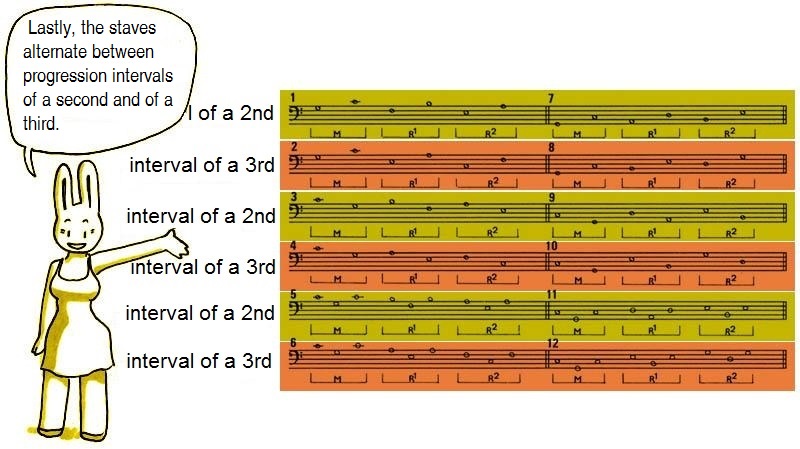
It
is important to note from the outset that the classification of a
sequence as descending (sequences nos 1-6) or as ascending (sequences
nos 7 to 12) implies a process of abstraction that
links classification to the succession of roots (such as:
C-F-B-E-A-D-G-C = descending sequence) in such a way that the ascending
or descending melodic orientation of the discourse itself, in one or
all of its components - due, for example, to a shift in octave, - may seem to contradict the classification:
Example 392 : J.S. Bach : Partita no 6, BWV 830, toccata (mm 99-101)
Type 1 sequence

Example 393 : L.V. Beethoven : Piano Sonata, op. 10, no 1 (mm 32-44)
Type 2 sequence

Example 394 : F. Schubert : Symphony no 9, D. 944, II, Andante con moto (mm 145-152)
Type 4 sequence

3. MELODIC FORMULATIONS: CHARACTERISTIC MOTIFS
