Through the lectures of Rosette Renshaw, a remarkable
and formidable pedagogue taught by Nadia Boulanger, I soon had at my
disposal a whole arsenal of prefabricated material consisting of a
collection of capsules of harmonic vocabulary (named as such, it seems,
by Nadia Boulanger). These formulas proved valuable in my first attempt
to grasp the harmonic reality from Bach to Wagner, but at the same time
I had to account for the presence of a latent, underlying, immanent principle to which Professor Renshaw referred us on occasion and which we found
sporadically in a few treatises on harmony in the form of a vague and
preliminary mention of an indisputable aphorism which in modern terms
could be stated thus:

It
was necessary to understand from the outset that
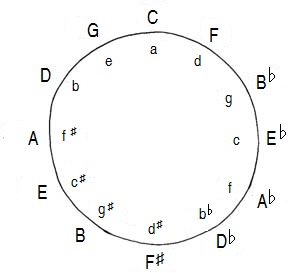
in this case, this maxim does not refer to the principle which governs
the relationships between consecutive tonalities in the tonal system by
ordering the sequence in which the sharps and flats appear (a
phenomenon which is reduced to what we call more precisely the
circle of fifths of tonalities or keys).
Figure 1
Rather,
it refers to the relationships between the chords belonging to a single
key, thus describing a circle of fifths of functions: I-IV-VII-III-VI-II-V-I.
Figure 2
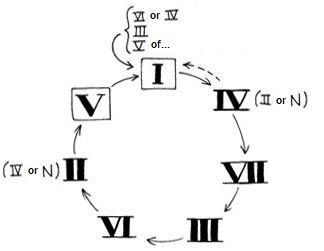
Figure 3

However, how is it possible to reconcile the systematic
order of this progression of functions with the reality of certain
formulas of harmonic vocabulary such as:
V - VI - IV - V - I
III - IV - V - I
V of IV - IV - V - I
I - IV - II - V - I
While I was painstakingly trying to resolve these
contradictions, the answer struck me like a bolt of lighting upon
meeting Richard Franko Goldman, or more precisely upon reading his
remarkable book Harmony in Western Music, published in 1965 by Norton in New
York. Here, Goldman accomplishes a masterful demonstration of the
pertinence of the descending circle of fifths as the foundational
structure of the harmonic discourse from Bach to Wagner. At the same
time, he addresses the most frequent discrepancies concerning this
structure and elaborates a theory capable of integrating these apparent
inconsistencies. Faced with the collection of harmonic formulas
inherited from Nadia Boulanger through Rosette Renshaw, I now held,
ready to be tested, the embryo of a solid and coherent explanatory
model that I then sought to develop and perfect.
